Регрессионный анализ

Вторым этапом изучения статистической связи вслед за определением степени тесноты связи с помощью коэффициента корреляции идет этап установления формы связи или вида функции φ(х), объясняющей основную закономерность влияния факторного признака х на результативный признак у.

Под формой статистической связи понимают ту тенденцию, которая проявляется в изменении изучаемого результативного признака в связи с изменением факторного признака. Форму связи можно попытаться установить, построив в прямоугольной системе координат все множество пар значений признаков (хi, уi), . По оси абсцисс откладываются значения факторного признака х, по оси ординат - значения признака у. Такое графическое построение называется полем корреляции или диаграммой рассеяния. По характеру расположения точек на координатной плоскости можно судить о характере статистической связи. Если наблюдается тенденция равномерного возрастания или убывания значений признака, то связь называется прямолинейной. При тенденции неравномерного изменения значений зависимость носит название криволинейной.

Линия на графике, изображающая тенденцию в изменении результативного признака при возрастании факторного, называется линией регрессии. В случае прямолинейной связи линия регрессии ищется в виде уравнения прямой линии:

,(3)

где у - теоретические значения результативного признака, образующие прямую линию; а0, а1 - параметры уравнения; х - значения факторного признака.

Расчет параметров уравнения производится методом наименьших квадратов. В основу метода положено требование минимальности отклонения теоретических значений у’i от эмпирических (полученных в результате наблюдения) значений признака уi при одном и том же значении хi. Это требование в математических обозначениях записывается следующим образом:

.(4)

Подставляя вместо теоретических значений их запись через параметры а0 и а1 , получаем

.(5)

В этом выражении известны все хi и уi, полученные в результате наблюдения, неизвестны лишь а0 и а1. Полученная функция двух переменных а0 и а1 имеет минимум, когда частные производные и одновременно равны 0. Произведя дифференцирование по а0 и а1, получаем систему двух уравнений с двумя неизвестными:

(6)

гдеn - общее число наблюдений; х, у - значения признаков, полученные в результате наблюдения.

Решая данную систему уравнений, получим выражение для нахождения коэффициентов а0 и а1:

,(7)

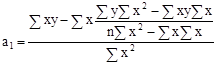,(8)

статистический цех корреляция регрессия

гдеn - общее число наблюдений; х, у - значения признаков, полученные в результате наблюдения.

Поля корреляции и уравнения регрессии для четырех цехов представлены на рис. 5-8.

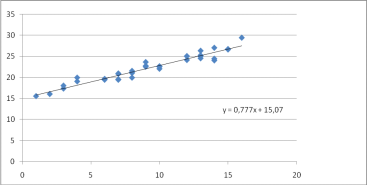
Рисунок 5 - Поле корреляции для характеристик оборудования первого цеха

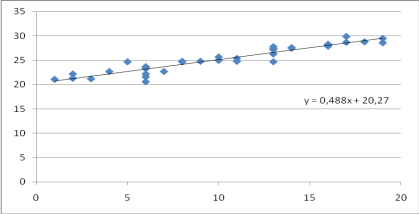
Рисунок 6 - Поле корреляции для характеристик оборудования второго цеха

Рисунок 7 - Поле корреляции для характеристик оборудования третьего цеха

Другие материалы

Статистические методы анализа оборотных фондов
В современном обществе важную роль в механизме управления экономикой выполняет статистика. Она осуществляет сбор, научную обработку, обобщение и анализ информации, характеризующей развитие экономики страны, культуры и уровня жизни населения. В р ...

Анализ производственно-хозяйственной деятельности на предприятии на примере ЗАО УИ ПДЭС
Обеспечение эффективного функционирования организаций требует экономически грамотного управления их деятельностью, которое во многом определяется умением ее анализировать. С помощью комплексного анализа изучаются тенденции развития, глубоко и си ...